문제
크기가 R×C인 목장이 있고, 목장은 1×1 크기의 칸으로 나누어져 있다. 각각의 칸에는 비어있거나, 양 또는 늑대가 있다. 양은 이동하지 않고 위치를 지키고 있고, 늑대는 인접한 칸을 자유롭게 이동할 수 있다. 두 칸이 인접하다는 것은 두 칸이 변을 공유하는 경우이다.
목장에 울타리를 설치해 늑대가 양이 있는 칸으로 갈 수 없게 하려고 한다. 늑대는 울타리가 있는 칸으로는 이동할 수 없다. 울타리를 설치해보자.
입력
첫째 줄에 목장의 크기 R, C가 주어진다.
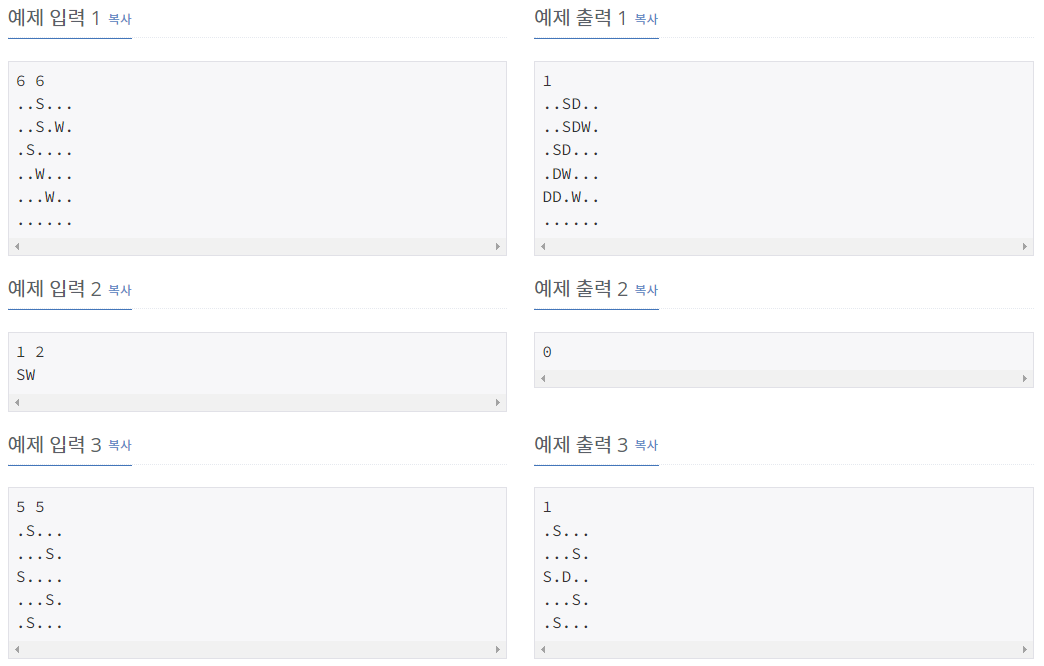
둘째 줄부터 R개의 줄에 목장의 상태가 주어진다. '.'는 빈 칸, 'S'는 양, 'W'는 늑대이다.
출력
늑대가 양이 있는 칸으로 갈 수 없게 할 수 있다면 첫째 줄에 1을 출력하고, 둘째 줄부터 R개의 줄에 목장의 상태를 출력한다. 울타리는 'D'로 출력한다. 울타리를 어떻게 설치해도 늑대가 양이 있는 칸으로 갈 수 있다면 첫째 줄에 0을 출력한다.
이 문제는 설치해야 하는 울타리의 최소 개수를 구하는 문제가 아니다.
- 1 ≤ R, C ≤ 500
반응형
풀이
R, C = map(int, input().split())
M = [list(input()) for _ in range(R)]
# 방향 벡터
dx, dy = [1, -1, 0, 0], [0, 0, 1, -1]
anw = True # 울타리를 칠 수 있으면 True, 없으면 False
# 늑대와 양이 만날 수 있는지 판단 (anw가 True or False인지)
for i in range(R):
for j in range(C):
if M[i][j] == 'W': # 늑대가 있는 칸이 있으면
for d in range(4): # d = direction, 늑대 기준으로 상하좌우 4방향을 탐색
i_, j_ = i + dx[d], j + dy[d]
# 늑대의 위치를 기준으로 탐색을 할 때, R,C 행렬 크기를 넘어선 부분을 탐색 시도하려고 하면, 무시하고 다음 for문 진행
if i_ < 0 or i_ == R or j_ < 0 or j_ == R:
continue
# 탐색한 위치에 양이 있는 경우, 울타리를 설치할 수 없으므로 anw = False가 됨.
if M[i_][j_] == 'S':
anw = False
# 출력을 위한 코드
if anw:
print(1)
for i in range(R):
for j in range(C):
if M[i][j] not in 'SW':
M[i][j] = 'D'
else:
print(0)
for data in M:
print(''.join(data))- 문제의 출력을 예제에서 주어진 것처럼 할 필요가 없음. 예제 출력3을 보면 울타리 D의 위치가 맥락이 없음.... 그래서 울타리를 칠 수 있는 공간은 모두 울타리가 있다고 출력할 것임. (틀렸다고 나오지 않음)
- 행렬에서, 늑대의 위치를 기준으로 상하좌우를 확인 (탐색)할 것임. (방향벡터, dx, dy = [1, -1, 0, 0], [0, 0, 1, -1] 사용)
- 늑대가 양을 만날 수 있는 구조인지 아닌지 판단한 뒤에, 출력을 위한 코드를 작성
출처
- 문제를 번역한 사람: baekjoon
'What is Computer? > Data structure & Algorithm' 카테고리의 다른 글
| [Python] 백준 '유기농 배추' 1012번 | 탐색, Flood fill, DFS 알고리즘 문제 (0) | 2022.10.11 |
|---|---|
| [Python] 백준 '꽃길' 14620번 | 방향 벡터, 브루트 포스, DFS 알고리즘 문제 (0) | 2022.10.11 |
| [Python] 백준 '친구 네트워크' 4195번 | 해시 Union-Find, 집합, 그래프 자료구조 문제 (0) | 2022.10.10 |
| [Python] 백준 '수 찾기' 1920번| 해쉬, 배열, 구현 자료구조 (0) | 2022.10.10 |
| [Python] 백준 'SHA-256' 10930번 | 해시, 구현 자료구조 문제 (0) | 2022.10.08 |
![[Python] 백준 '늑대와 양' 16956번 | 방향벡터 알고리즘 문제](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FD2EDr%2FbtrN9k3084l%2FAAAAAAAAAAAAAAAAAAAAAIKjNh8LapB4NmqGa7YRXuWoYJVEVYHxYUZVD9kslodD%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1767193199%26allow_ip%3D%26allow_referer%3D%26signature%3Dd8cUyrt2iAm7KB58pHnOe9z94pQ%253D)